Affine rectification from pairs of parrallel lines

perform an affine rectification of an image. Given two pairs of image of parallel lines, the script find the image of the line at infinity as the ones passing through the vanishing points. The homography that maps the line at infinity to its canonical form: (0: 0: 1) rectify the image up to an affinity transformation.

Luca Magri
Politecnico di Milano
2020

Contents

load the image

clear;
close all;
img = imread('images/img1.JPG');
figure; imshow(img);
title('Draw two pairs of parallel segments and press enter')

select two pairs of segments that are image of parallel lines in the scene

fprintf('Draw parallel segments\n');

% select a first pair of segments (images of 2 parallel lines)
segment1 = drawline('Color','red');
segment2 = drawline('Color','red');


% select a second pair of segments (images of 2 parallel lines)
segment3 = drawline('Color','blue');
segment4 = drawline('Color','blue');

fprintf('Press enter to continue\n');
pause

Draw parallel segments
Press enter to continue

compute the image of the line at infinity

l1 = segToLine(segment1.Position);
l2 = segToLine(segment2.Position);

m1 = segToLine(segment3.Position);
m2 = segToLine(segment4.Position);

% compute the vanishing points
L = cross(l1,l2);
L = L./L(3);
M = cross(m1,m2);
M = M./M(3);

% compute the image of the line at infinity
imLinfty = cross(L,M);
imLinfty = imLinfty./(imLinfty(3));

% dispaly the selection
figure;
hold all;
% plot vanishing points
plot(L(1),L(2),'r.','MarkerSize',100);
plot(M(1),M(2),'b.','MarkerSize',100);
imshow(img);
% plot vanishing line
line([L(1),M(1)],[L(2),M(2)],'Color','Green','Linewidth',3);
% plot selected segments
line([segment1.Position(1,1),segment1.Position(2,1)],[segment1.Position(1,2),segment1.Position(2,2)],'Color','red','Linewidth',3);
line([segment2.Position(1,1),segment2.Position(2,1)],[segment2.Position(1,2),segment2.Position(2,2)],'Color','red','Linewidth',3);
line([segment3.Position(1,1),segment3.Position(2,1)],[segment3.Position(1,2),segment3.Position(2,2)],'Color','blue','Linewidth',3);
line([segment4.Position(1,1),segment4.Position(2,1)],[segment4.Position(1,2),segment4.Position(2,2)],'Color','blue','Linewidth',3);
hold off;
legend('Vanishing point 1', 'Vanishing point 2','Image of l_\infty');
set(gca,'FontSize',20)

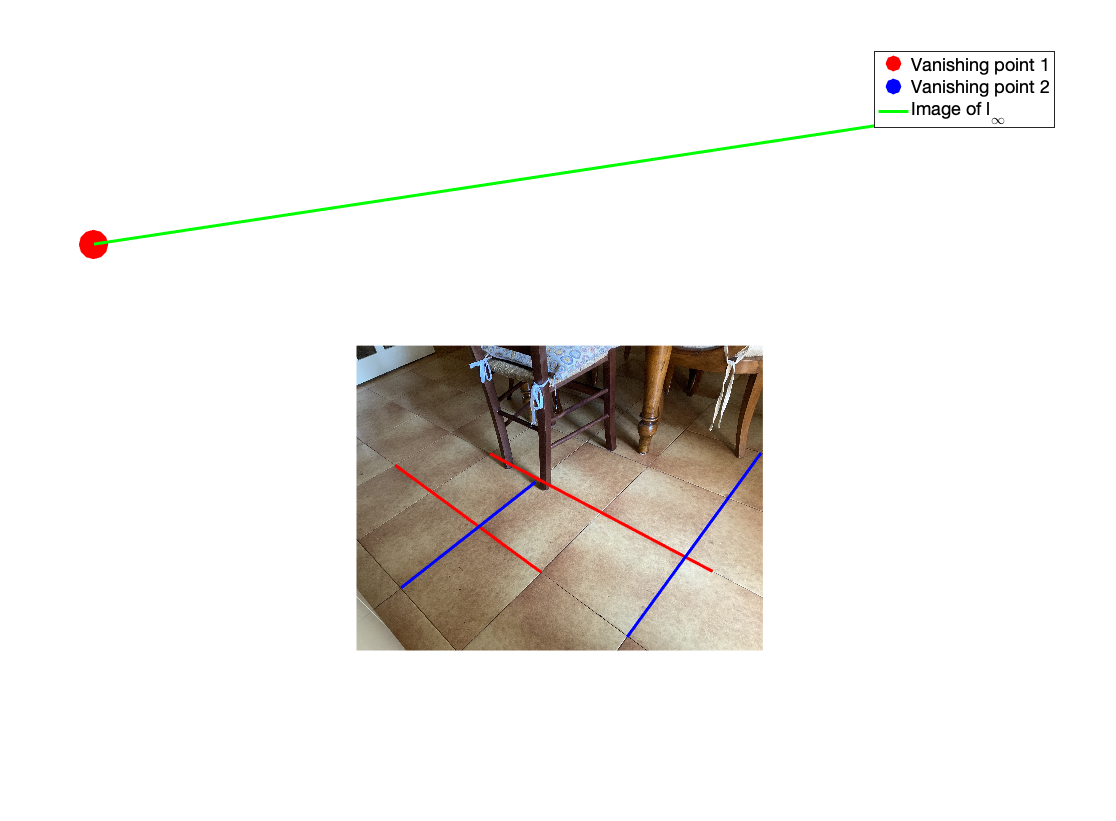
build the rectification matrix

H = [eye(2),zeros(2,1); imLinfty(:)'];
% we can check that H^-T* imLinfty is the line at infinity in its canonical
% form:

% compute the rectifying matrix
fprintf('The vanishing line is mapped to:\n');
disp(inv(H)'*imLinfty);

The vanishing line is mapped to:
     0
     0
     1

rectify the image and show the result

tform = projective2d(H');
J = imwarp(img,tform);

figure;
imshow(J);
imwrite(J,'images/affRect.JPG');






function [l] = segToLine(pts)
% convert the endpoints of a line segment to a line in homogeneous
% coordinates.
%
% pts are the endpoits of the segment: [x1 y1;
%                                       x2 y2]

% convert endpoints to cartesian coordinates
a = [pts(1,:)';1];
b = [pts(2,:)';1];
l = cross(a,b);
l = l./norm(l);
end

Published with MATLAB® R2020a