drawcubeiso

A simple geometrical construction with 2D homogeneous coordinates
Naming
Data entering
Finding some lines
Check the incidence equation
Parallelism
Finding remaining points
Drawing
Notes

A simple geometrical construction with 2D homogeneous coordinates

Our goal is to complete the drawing of the isometric projection http://en.wikipedia.org/wiki/Isometric_projection of a cuboid when the points corresponding to a vertex and to three vertices adjacent to it are given as input. The geometrical construction only requires to find lines parallel to other lines, find lines passing through two points, and intersect lines, which is easily achieved in homogeneous coordinates.

clear
close all
clc

Naming

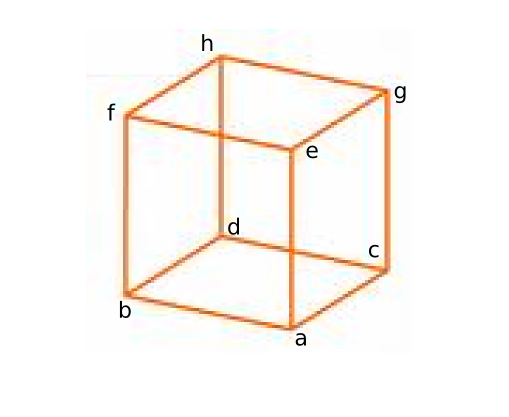
We will name the vertices as in the following image

figure(1), imshow(imread('simplecube-letters.png'));
FNT_SZ = 28;

Data entering

the user should click on a vertex of the cuboid, then on the three adjacent vertices

figure(2),
imshow(imread('buildingSmall.png'))
% imshow(imread('cube.jpeg'))
hold on;
[x y]=getpts
plot(x,y,'.w','MarkerSize',12, 'LineWidth', 3); % plots points clicked by user with red circles
a=[x(1) y(1) 1]';
text(a(1), a(2), 'a', 'FontSize', FNT_SZ, 'Color', 'w')
b=[x(2) y(2) 1]';
text(b(1), b(2), 'b', 'FontSize', FNT_SZ, 'Color', 'w')
c=[x(3) y(3) 1]';
text(c(1), c(2), 'c', 'FontSize', FNT_SZ, 'Color', 'w')
e=[x(4) y(4) 1]';
text(e(1), e(2), 'e', 'FontSize', FNT_SZ, 'Color', 'w')

Finding some lines

Now variables a, b, c and d are 3-vectors containing the homogeneous coordinates of the 2D points. We need to find the lines passing through couples of points, using the cross product

lab=cross(a,b)
lac=cross(a,c)
lae=cross(a,e)

lab =
   1.0e+04 *
    0.0024
   -0.0093
    4.2051
lac =
   1.0e+04 *
    0.0091
    0.0060
   -7.4515
lae =
   1.0e+05 *
    0.0025
    0.0000
   -1.1194

Check the incidence equation

lab, lac and lae now contain the homogeneous represenation of the three lines ab, ac and ae. We can easily check that the lines actually contain the points by using the incidence relation:

lab'*a
lab'*b
lac'*a
lac'*c
lae'*a
lae'*e

ans =
  -1.4552e-11
ans =
  -1.4552e-11
ans =
     0
ans =
     0
ans =
  -1.4552e-11
ans =
  -1.4552e-11

Parallelism

We now need to compute the line parallel to ab and passing through c. In order to do this, we create the line at infinity:

linf=[0 0 1]';

then, we find the directions of segments by ab, ac and ae intersecting their lines with the line at infinity

dab=cross(lab,linf)
dac=cross(lac,linf)
dae=cross(lae,linf)

dab, dac and dae are points at the infinity, which represent directions. All lines with a given direction pass through the corresponding point at the infinity. We can then find the lines containing segments bd and cd.

lbd=cross(b,dac);
lcd=cross(c,dab);

point d is now found by just intersecting lbd and lcd

d=cross(lbd,lcd);

we normalize d's coordinates so that we can read its cartesian coordinates in d(1) and d(2). We plot the point with a blue circle.

d=d/d(3);
plot(d(1),d(2),'.b','MarkerSize',12);
text(d(1), d(2), 'd', 'FontSize', FNT_SZ, 'Color', 'w')

Finding remaining points

The rest of the procedure is straightforward, and follows exactly the same technique.

lbf=cross(b,dae);
lcg=cross(c,dae);
ldh=cross(d,dae);
lef=cross(e,dab);
leg=cross(e,dac);

f=cross(lbf,lef);
g=cross(lcg,leg);

lfh=cross(f,dac);
h=cross(lfh,ldh);

f=f/f(3);
g=g/g(3);
h=h/h(3);

plot(f(1), f(2),'.w','MarkerSize',12, 'LineWidth', 3); % plots points clicked by user with red circles
text(f(1), f(2), 'f', 'FontSize', FNT_SZ, 'Color', 'w')
plot(g(1), g(2),'.w','MarkerSize',12, 'LineWidth', 3); % plots points clicked by user with red circles
text(g(1), g(2), 'g', 'FontSize', FNT_SZ, 'Color', 'w')
plot(h(1), h(2),'.w','MarkerSize',12, 'LineWidth', 3); % plots points clicked by user with red circles
text(h(1), h(2), 'h', 'FontSize', FNT_SZ, 'Color', 'w')

Drawing

we can now finally draw the cube.

myline=[a';b';d';c';a'];
line(myline(:,1),myline(:,2),'LineWidth',5);
myline=[e';f';h';g';e'];
line(myline(:,1),myline(:,2),'LineWidth',5);
myline=[a';e'];
line(myline(:,1),myline(:,2),'LineWidth',5);
myline=[b';f'];
line(myline(:,1),myline(:,2),'LineWidth',5);
myline=[c';g'];
line(myline(:,1),myline(:,2),'LineWidth',5);
myline=[d';h'];
line(myline(:,1),myline(:,2),'LineWidth',5);
hold off

Notes

which vertices you click is not important: the only requirement is that the first vertex is adjacent to the other three. also, note that the algorithm works, more generally, on parallelepipeds.

Contents