Contents

Basic experiments with conic sections in homogeneous coordinates

clc
clear
close all

Define a circumference

Let's define circumference centered in 0,0 with radius 200 x^2 + y^2 = 200^2 % circumference

r=200
C=[1 0 0; 0 1 0; 0 0 -r^2]

% or more in general...
a = 1;
b = 0;
c = 1;
d = 0;
e = 0;
f = -r^2;

C=[a, b/2, d/2; b/2, c, e/2; d/2 e/2 f];

% the conic equation is x'Cx = 0

r =

   200


C =

           1           0           0
           0           1           0
           0           0      -40000

sample the conics

we evaluate x'*C*x at different points in the plane (here pixels) x * C * x' = 0 is the incidence relation

im = zeros(500, 500);
for ii = 1 : 500
    for jj = 1 : 500
        im(ii, jj) = [jj, ii, 1] * C * [jj; ii; 1];
    end
end

visualization

% Show the actual values at each pixel: the smallest value will be black
% and the biggest one will be white.
figure(), imshow(im,[]), title('sampling x^T * C * x');

% We are interested in where the values are greater than zero or less than
% zero. Points "inside" the circumference yield values that are negative
% outside instead the values are positive
figure(), imshow(im>0), title('outside the circumference')

% the values of x'*C*x identify a 3D paraboloid whose intersection with the
% plane z = 0 gives the circumference (the same holds for other conics)
figure(), mesh(im), title('3D visualization, the circumference is the intersection with z = 0')
colormap jet
view(gca,[-49.5 13.2]);

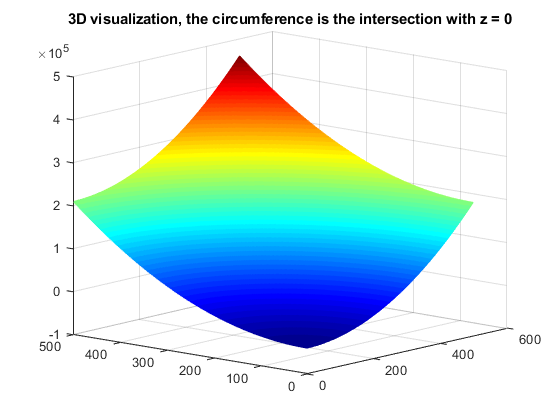
Some transformations

Let's move the circumference to the center of the image, and scale it to half size. We will build a similarity transform

t=[250 250]';   % translation
s=0.5;           % scale factor
Similarity = [s * eye(2) t; 0 0 1];

We transform the conic...

Cprime=inv(Similarity)'*C*inv(Similarity);

.. and we draw it as before:

im=zeros(500,500);
for i=1:500
    for j=1:500
        im(i,j)=[j i 1]*Cprime*[j i 1]';
    end
end

imshow(im>0), title('shifted circumference')

figure(), mesh(im), title('3D visualization, the circumference is the intersection with z = 0')
colormap jet
view(gca,[-49.5 13.2]);

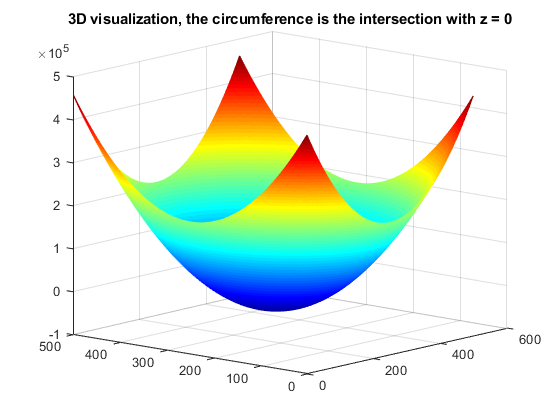
Obviously, the line at the infinity is unchanged by our similarity

inv(Similarity)'*[0 0 1]'

ans =

     0
     0
     1

Published with MATLAB® R2017b