|
Foveated Self-Similarity in Nonlocal Image Processing
Introduction When we gaze a scene, our visual acuity is maximal at the fixation point, which is imaged in the fovea, and decreases rapidly towards the periphery of the visual field. This phenomenon is known as foveated vision or foveated imaging. We investigate the role of foveation in nonlocal image filtering.
Figure 1 An illustrative example of how foveated images look like. Because of the uneven size and organization of photo-receptive cells and ganglions in the human eye, the visual acuity and the sharpness of the retinal image is highest in the fovea, the central part of the retina, where the concentration of cones has its peak. At the periphery of the retina, vision is instead blurry. Foveated Self-Similarity Inspired by the human visual system, we design foveation operators to reproduce the foveation effects on image patches, and we consider the foveated distance, i.e., the Euclidean distance between foveated patches, as a measure of nonlocal self-similarity in natural images. If we consider the patch center as a fixation point, the foveated distance mimics the inability of the human visual system to perceive details at the periphery of the center of attention. We adopt image denoising as a techinque to quantitatively assess the effectiveness of such a prior for natural images. Foveated NL-Means
We introduce Foveated NL-means, a modification over the classical NL-means [Buades et al 2005], where the patch similarity is measured by the foveated patch distance, i.e., the Euclidean distance between foveated patches instead of the conventional windowed distance. Foveated NL-means achieves substantial improvement in the denoising quality over the standard NL-means, according to both objective criteria and visual appearance, particularly due to better contrast and sharpness. Detailed results are presented in [Foi and Boracchi, 2016].
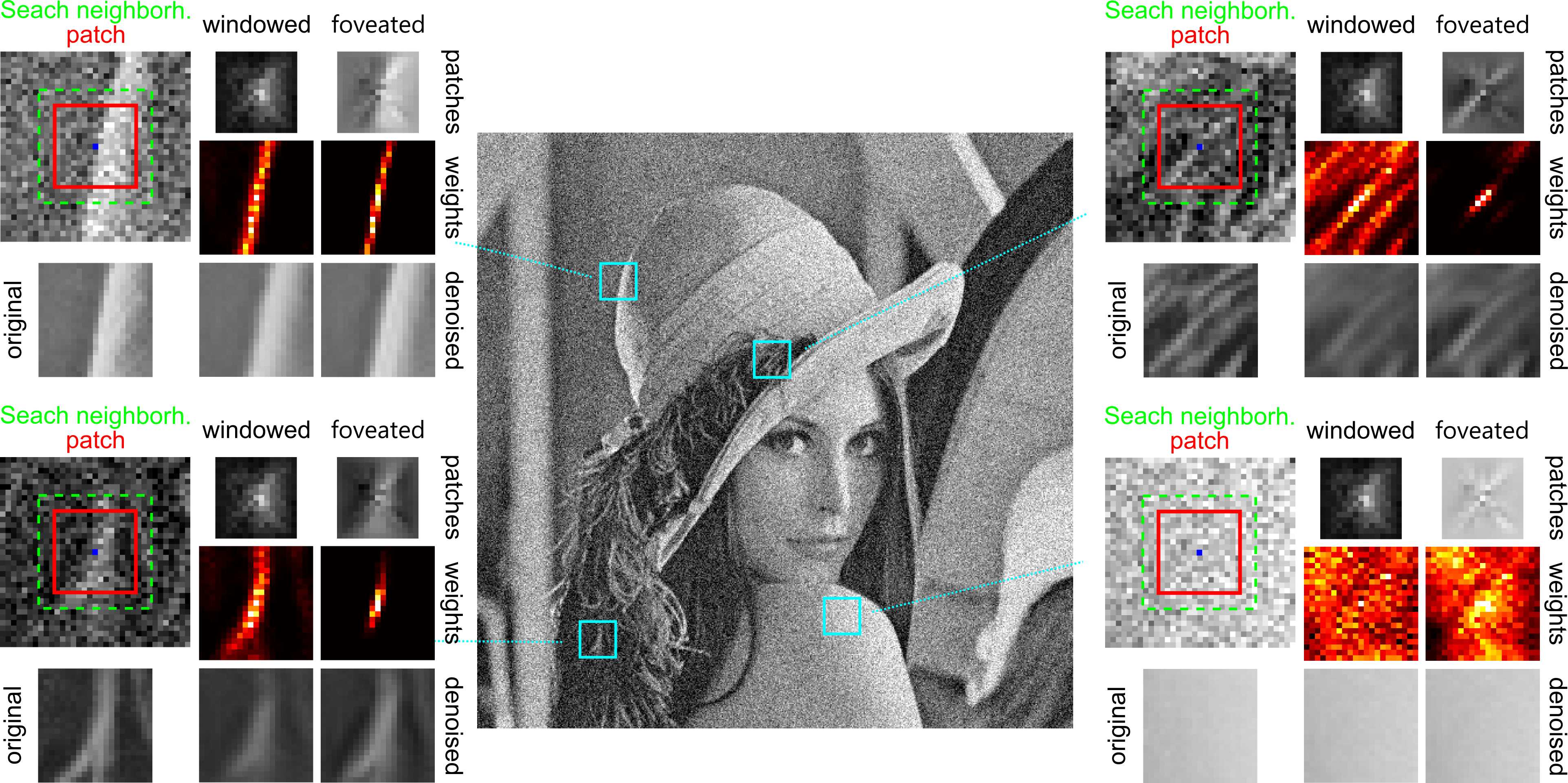
Figure 2 Details of four patches taken from noisy Lena corrupted by AWGN (standard deviation 50). For each noisy patch (dashed green line), we report the center (blue dot), the corresponding search neighborhood (dashed green line), the windowed patch, and the foveated patch. These patches are used for computing the displayed NL-means weights over the search neighborhood. These weigths give the pixelwise denoised estimates and, for the sake of visualization, we display all the denoised estimates in to the whole search neighborhood. Foveation preserves better than windowing the original image structures: the weights from foveated distance are better localized around edges, details and textures and yield the best estimates in terms of sharpness, contrast, and overall visual quality. We motivate the superior performance of Foveated NL-means in terms of low level vision: the foveated self-similarity is a far more effective regularization prior for natural images than the conventional windowed self-similarity. Resources |
|
References [Foi and Boracchi, 2016] Foveated Nonlocal Self-Similarity [Buades et al. 2005] A review of image denoising algorithms, with a new one. [Foi and Boracchi, 2012] Foveated self-similarity in nonlocal image filtering [Foi and Boracchi, 2013a] Anisotropic Foveated Self-Similarity [Foi and Boracchi, 2013b] Anisotropically Foveated Nonlocal Image Denoising |